McCumber relation
The McCumber relation (or McCumber theory) refers to the effective cross-sections of absorption and emission of light in the physics of solid-state lasers [1][2].
Contents |
Definition
Let 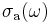 be the effective absorption cross-section
be the effective absorption cross-section 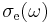 be effective emission cross-sections at frequency
be effective emission cross-sections at frequency  , and let
, and let 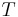 be the effective temperature of the medium. The McCumbner relation is
be the effective temperature of the medium. The McCumbner relation is
- (1)
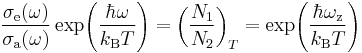
where 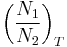 is thermal steady-state ratio of populations; frequency
is thermal steady-state ratio of populations; frequency 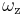 is called "zero-line" frequency [3][4];
is called "zero-line" frequency [3][4]; 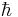 is the Planck constant and
is the Planck constant and 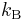 is the Boltzmann constant. Note that the right-hand side of Equation (1) does not depend on
is the Boltzmann constant. Note that the right-hand side of Equation (1) does not depend on 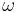 .
.
Gain
It is typical that the lasing properties of a medium are determined by the temperature and the population at the excited laser level, and are not sensitive to the method of excitation used to achieve it. In this case, the absorption cross-section 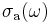 and the emission cross-section
and the emission cross-section 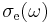 at frequency
at frequency 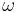 can be related to the lasers gain in such a way, that the gain at this frequency can be determined as follows:
can be related to the lasers gain in such a way, that the gain at this frequency can be determined as follows:
- (2)
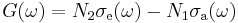
D.E.McCumber had postulated these properties and found that the emisison and absorption cross-sections are not independent [1][2]; they are related with Equation (1).
Idealized atoms
In the case of an idealized two-level atom the detailed balance for the emission and absorption which preserves the Max Planck formula for the black body radiation leads to equality of cross-section of absorption and emission. In the solid-state lasers the splitting of each of laser levels leads to the broadening which greatly exceeds the natural spectral linewidth. In the case of an ideal two-level atom, the product of the linewidth and the lifetime is of order of unity, which obeys the Heisenberg uncertainty principle. In solid-state laser materials, the linewidth is several orders of magnitude larger so the spectra of emission and absorption are determined by distribution of excitation among sublevels rather than by the shape of the spectral line of each individual transition between sublevels. This distribution is determined by the effective temperature within each of laser levels. The McCumber hypothesis is that the distribution of excitation among sublevels is thermal. The effective temperature determines the spectra of emission and absorption ( The effective temperature is called a temperature by scientists even if the excited medium as whole is pretty far from the thermal state )
Deduction of the McCumber relation
Consider the set of active centers (fig.1.). Assume fast transition between sublevels within each level, and slow transition between levels. According to the McCumber hypothesis, the cross-sections 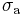 and
and 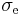 do not depend on the populations
do not depend on the populations 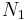 and
and 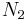 . Therefore, we can deduce the relation, assuming the thermal state.
. Therefore, we can deduce the relation, assuming the thermal state.
Let 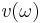 be group velocity of light in the medium, the product
be group velocity of light in the medium, the product 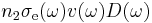 is spectral rate of stimulated emission, and
is spectral rate of stimulated emission, and 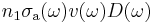 is that of absorption;
is that of absorption; 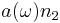 is spectral rate of spontaneous emission. (Note that in this approximation, there is no such thing as a spontaneous absorption) The balance of photons gives:
is spectral rate of spontaneous emission. (Note that in this approximation, there is no such thing as a spontaneous absorption) The balance of photons gives:
- (3)
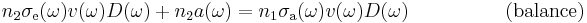
Which can be rewritten as
- (4)
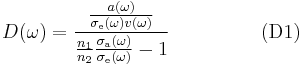
The thermal distribution of density of photons follows from blackbody radiation [5]
- (5)
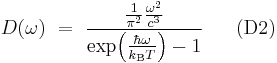
Both (4) and (5) hold for all frequencies 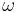 . For the case of idealized two-level active centers,
. For the case of idealized two-level active centers,  , and
, and 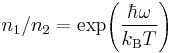 , which leads to the relation between the spectral rate of spontaneous emission
, which leads to the relation between the spectral rate of spontaneous emission 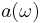 and the emission cross-section
and the emission cross-section 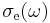 [5]. (We keep the term probability of emission for the quantity
[5]. (We keep the term probability of emission for the quantity 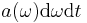 , which is probability of emission of a photon within small spectral interval
, which is probability of emission of a photon within small spectral interval 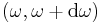 during a short time interval
during a short time interval 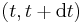 , assuming that at time
, assuming that at time 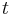 the atom is excited.) The relation (D2) is a fundamental property of spontaneous and stimulated emission, and perhaps the only way to prohibit a spontaneous break of the thermal equilibrium in the thermal state of excitations and photons.
the atom is excited.) The relation (D2) is a fundamental property of spontaneous and stimulated emission, and perhaps the only way to prohibit a spontaneous break of the thermal equilibrium in the thermal state of excitations and photons.
For each site number 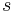 , for each sublevel number
, for each sublevel number  , the partial spectral emission probability
, the partial spectral emission probability 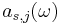 can be expressed from consideration of idealized two-level atoms [5]:
can be expressed from consideration of idealized two-level atoms [5]:
- (6)

Neglecting the cooperative coherent effects, the emission is additive: for any concentration 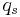 of sites and for any partial population
of sites and for any partial population 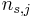 of sublevels, the same proportionality between
of sublevels, the same proportionality between 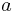 and
and 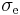 holds for the effective cross-sections:
holds for the effective cross-sections:
- (7)

Then, the comparison of (D1) and (D2) gives the relation
- (8)
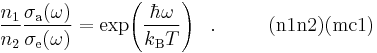
This relation is equivalent of the McCumber relation (mc), if we define the zero-line frequency 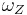 as solution of equation
as solution of equation
- (9)
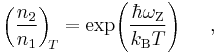
the subscript 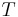 indicates that the ratio of populations in evaluated in the thermal state. The zero-line frequency can be expressed as
indicates that the ratio of populations in evaluated in the thermal state. The zero-line frequency can be expressed as
- (10)
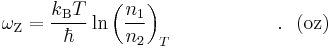
Then (n1n2) becomes equivalent of the McCumber relation (mc).
No specific property of sublevels of active medium is required to keep the McCumber relation. It follows from the assumption about quick transfer of energy among excited laser levels and among lower laser levels. The McCumber relation (mc) has the same range of validity as the concept of the emission cross-section itself.
Confirmation of the McCumber relation
The McCumber relation is confirmed for various media [6][7]. In particular relation (1) makes it possible to approximate two functions of frequency, emission and absorption cross sections, with single fit [8].
Violation of the McCumber relation and perpetual motion
In 2006 the strong violation of McCumber relation was "observed" for Yb:Gd2SiO5 and reported in 3 independent journals[9][10][11]. Typical behaivor of the cross-sections reported is shown in FIg.2 with thick curves. The emission cross-section is practically zero at wavelength 975 nm; this property makes Yb:Gd2SiO5 an excellent material for efficient solid-state lasers.
However, the property reported (thick curves) is not compatible with the Second Law of thermodynamics. With such a material, the Perpetual motion device would be possible. It would be sufficient to fill a box with reflecting walls with Yb:Gd2SiO5 and allow it to exchange radiation with a blackbody through a spectrally-selective window which is transparent in vicinity of 975 nm and reflective at other wavelengths. Due to the lack of emissivity at 975 nm the medium should warm, breaking the thermal equilibrium.
On the base of the Second Law of thermodynamics, the experimental results [9][10][11] were refuted in 2007. WIth the McCumner theory, the correction was suggested for the effective emission cross section (black thin cirve) [3]. Then this correction was confirmed experimentally[12].
References
- ^ a b D.E.McCumber. Einstein relations connecting broadband emission and absorption spectra. PRB 136 (4A), 954–957 (1964)
- ^ a b P.C.Becker, N.A.Olson, J.R.Simpson. Erbium-doped fiber amplifiers: fundamentals and theory (Academic, 1999).
- ^ a b D. Kouznetsov (2007). "Comment on Efficient diode-pumped Yb:Gd2SiO5 laser (Appl.Phys.Lett.88,221117(2006))". APL 90: 066101. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=APPLAB000090000006066101000001&idtype=cvips&gifs=yes.
- ^ D.Kouznetsov (2007). "Broadband laser materials and the McCumber relation" (– Scholar search). Chinese Optics Letters 5: S240–S242. http://col.org.cn/getArticle.aspx?id=OJ070715000250D0GcIf.
- ^ a b c e2
- ^ R.S.Quimby (2002). "Range of validity of McCumber theory in relating absorption and emission cross sections". J. Appl. Phys. 92: 180–187. Bibcode 2002JAP....92..180Q. doi:10.1063/1.1485112. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=JAPIAU000092000001000180000001.
- ^ R.M.Martin; R.S.Quimby (2006). "Experimental evidence of the validity of the McCumber theory relating emission and absorption for rare-earth glasses". JOSAB 23 (9): 1770–1775. Bibcode 2006JOSAB..23.1770M. doi:10.1364/JOSAB.23.001770. http://josab.osa.org/abstract.cfm?id=97826.
- ^ D.Kouznetsov; J.-F.Bisson, K.Takaichi, K.Ueda (2005). "Single-mode solid-state laser with short wide unstable cavity". JOSAB 22 (8): 1605–1619. Bibcode 2005JOSAB..22.1605K. doi:10.1364/JOSAB.22.001605. http://josab.osa.org/abstract.cfm?id=84730.
- ^ a b W. Li; H. Pan, L. Ding, H. Zeng, W. Lu, G. Zhao, C. Yan, L. Su, J. Xu. (2006). "Efficient diode-pumped Yb:Gd2SiO5 laser". APL 88: 221117. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=APPLAB000088000022221117000001.
- ^ a b W.Li; H.Pan, L.Ding, H.Zeng, G.Zhao, C.Yan, L.Su, J.Xu (2006). year=2006 "Diode-pumped continuous-wave and passively mode-locked Yb:Gd2SiO5laser". Optics Express 14 (2): 686–695. Bibcode 2006OExpr..14..686L. doi:10.1364/OPEX.14.000686. http://www.opticsexpress.org/search.cfm year=2006.
- ^ a b C.Yan; G.Zhao, L.Zhang, J.Xu, X.Liang, D.Juan, W.Li, H.Pan, L.Ding, H.Zeng. (2006). "A new Yb-doped oxyorthosilicate laser crystal: Yb:Gd2SiO5". Solid State Communications 137 (8): 451–455. Bibcode 2006SSCom.137..451Y. doi:10.1016/j.ssc.2005.12.023. http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6TVW-4HYTYFW-3&_user=10&_coverDate=02%2F28%2F2006&_alid=615430684&_rdoc=1&_fmt=summary&_orig=search&_cdi=5545&_sort=d&_docanchor=&view=c&_ct=1&_acct=C000050221&_version=1&_urlVersion=0&_userid=10&md5=b6673cac47762a0184b56a206d31ccd6.
- ^ G.Zhao; L.Su, J.Xua, and H.Zeng (2007). "Response to Comment on Efficient diode-pumped Yb:Gd2SiO5 laser (Appl. Phys. Lett. 90, 066101 2007)". APL 90: 066103. http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=APPLAB000090000006066103000001&idtype=cvips&gifs=yes.